SECTION A
Answer all questions in this section

1. Factorize :(x+4)² -(x-3)²

2. Solve the simultaneous equations
        2x-3y-7=0
        x+4y+2=0

3.The table below shows marks obtained by 34 students in a Chemistry test. Calculate the mean mark.

4.Given that s*t=2s² – 3t, evaluate 6*(5*2)

5. An interior angle of a regular polygon is 162⁰. Find the sum of its interior angles.

6.Find the values of x and y in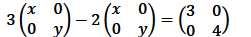

7. Solve for x in the inequality ½ - ⅔ x< ⅙ x- ¼

8. In the right angled triangle ABC below, AB = 10cm and AC = 6cm

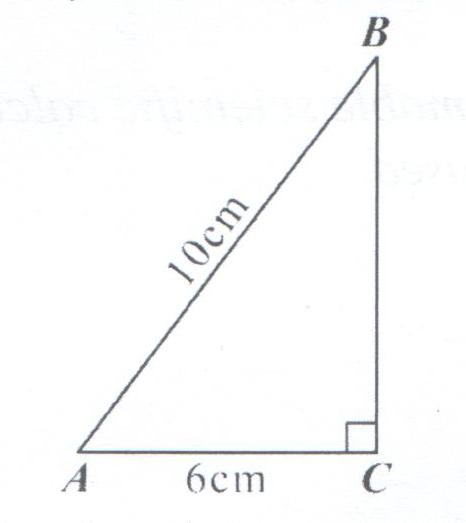
Determine the;
a) Length of BC
b) area of triangle ABC

9. A number which is divisible by 3 is chosen at random from a set of even numbers between 1     and 20. What is the probability of choosing the number?

10. The graph below shows the line HK and its image Hʹ Kʹīī after a rotation in the clockwise direction.

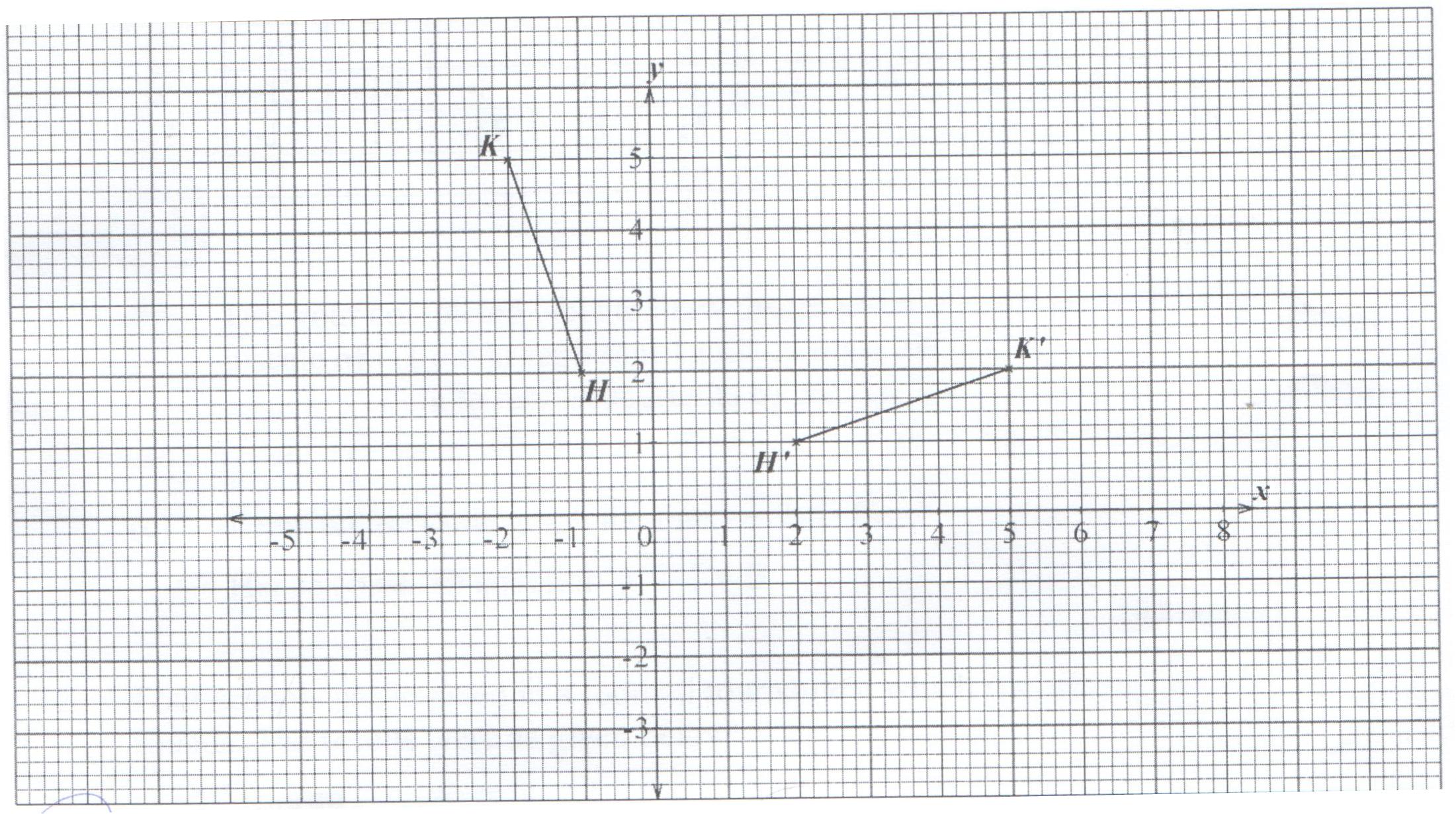
Use the graph to determine the;
coordinates of the centre of rotation
angle of rotation

SECTION B
Answer any five questions from this section. All questions carry equal marks.

11.Copy and complete the table of values below for y = x²+ 2x - 15.

a) Use your completed table to draw the graph of y=x²+2x-15. Use a scale of: 1cm to represent 1 unit on the x-axis, 1cm to represent 2 units on the y- axis.

b) Draw on the same graph the line y = 2x-14
Hence solve the equation x²-1=10.

12. Four schools participated in a football tournament which was played in two rounds. The results were as given below;

1st Round
- Bakulu S.S won one, drew three and lost two matches
- Dodo S,S won two, drew two and lost two matches.
- Kawunga S,S won three, drew two and lost four matches.

2nd Round
- Bakulu S,S won one, drew two and lost three matches
- Dodo S,S won two, drew one and lost three matches
- Kawunga S,S won two, drew three and lost one match
- Oronga S,S won one, drew four and lost one match.

a) Write down a 4 × 3 matrix which shows the performance of the schools in
     i) each of the two rounds
     ii) both rounds
b) Three points are awarded for a win, one point for a draw and no point for a loss.
     i) Write down a 3× 1 matrix to represent the award of pointsʹ
     ii) Using matrix multiplication, determine which school won the tournament.

13.a) Make D the subject of the expression

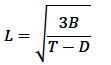
Hence, find the value of D when B = 540, L =18 and T = 17
b) Auma bought 5 sackets of washing powder and a tube of toothpaste at shs1,700 in January. In February she bought 15 sackets of washing powder and 2 tubes of toothpaste at Shs4,400. What was the price of each item during the two months?

Using a ruler, a pencil and a pair of compasses only,
construct a triangle ABC, where angle ABC = 750, AB ̅ = 9.3cm, BC ̅ = 8.7cm

 b) Measure the length of AC ̅ and angle ACB

c) i) Draw an inscribed circle in the triangle ABC

    ii) Find the radius of the circle

15. A cupboard has 5 white cups and 3 black cups. Two cups are picked from the cupboard one after the other without replacement.

a) Draw a tree diagram to represent the given information

b) Calculate the probability of picking :

     i) one white cup and one black cup
     ii) two cups of the same color
     iii) at least one white cup

16. A triangle whose vertices are P,Q and R is mapped on a triangle whose vertices 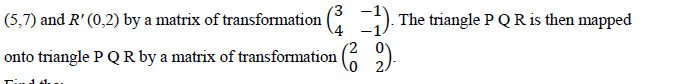Find the;

a) coordinates of Pʹʹ Qʹʹ and Rʹʹ

b) single matrix of transformation which would map Pʹʹ Qʹʹ Rʹʹ back onto PQR.

c)coordinates of Pʹʹ Qʹʹ and Rʹʹ

17. An investor wants to buy 2 types of generators A and B. Generator A needs 2 m² of space and B needs 3m². The available space is only 60m². The cost of A is £2,000 and that of B is £10,000. The investor has £80,000 to be spent. If x and y represent number of generators of type A and B respectively,

a) write down four inequalities from the information given

b) represent the four inequalities on the same axes.

c) find the greatest number of generators of both types A and B that the investor can buy using the minimum amount of money

END