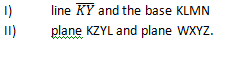SECTION A
Answer all questions in this section
1. An increase of 15% in salaries makes the monthly expenditure on salaries for a factory to be Shs22, 425,000.   Find the expenditure before the increase.

2. The sets M and P are such that n (M) =50, n(P)=25 and n(M∪P)=60. Calculate n (P∩M).

3. Find the equation of the line joining the points (3,5) and (-2,10).

4. A metallic cylindrical pipe of uniform cross-sectional area has an outer radius of 14cm and an inner radius of 6.5cm. It has a length of 4.2 meters. Calculate the volume in cm3, of the metal used to make the pipe.

5. Express

6. Given that, 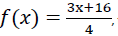 find the value of f ¹(1).

7.The coordinated of the mid-point of a line PQ are (8, -1). The coordinates of P are (5,-5). Determine the coordinates of Q.

8. Two water tanks are the same shape. The larger tank is 80cm high with a capacity of 500litres. What is the capacity of the smaller tank whose height is 48cm?

9. Fauza bought one dozen of the shirts at Shs 40,000 per shirt. She sold them at a profit of 20%. How much money did she earn as profit from the shirt sales?

10. In the figure below, OP =a, OQ =b and PR =⅓PQ

Express OR in terms of a and b

SECTION B

Answer any five questions from this section. All questions carry equal marks.

11. a) Simplify: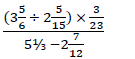

b) A forest reserve covering an area of 807.5km2 is represented on a map by a green area of 32.3cm². Determine the scale of the map.

12.In a survey carried out in the department of languages at a certain University, the following data was collected: 20 students spoke German. 10 spoke French and German. 9 spoke French and Kiswahili. 7 spoke Kiswahili and German only. 2 could not speak any of the three languages. 22 could speak at least two of the languages. 12 could speak only one language. 11 could either speak Kiswahili or German but not French.

a) Use a Venn diagram to represent the given information.

b) Find the number of students that could speak;

i) all the three languages
ii) Kiswahili only
iii)French only

c) What is the probability that a student picked at random from the group could speak neither Kiswahili nor German?

A cyclist covered a journey of 48km from station A to station B in 5½hrs. The cyclist rode at 12km/hr for the 2½hrs and changed speed for the remaining part of the journey.

a) i) Determine the speed of the cyclist for the remaining part of the journey.

    ii) Represent the cyclist journey on a distance – time graph.
b) Calculate the average speed of the cyclist from station A to B

14a) Given the set {2,4,6} draw a papyram to show the “is the smallest prime factor of.”

b) For the mapping x→ 4x+5, find the domain when the range is {1,13}.

c) The function f(x)=2x2 and g(x)=5x-3. Find the value of x such that f(x)= g(x)

15 a) If
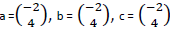          and 2a +m+b = c,
     i) m

    ii) |m|

b) Using vectors, show that the points P(-4,1), Q(0,2) and R(8,4) lie on a straight line.

The table below shows fares for some flights at an airport.

One way ticket means from airport to destination
Return ticket means from airport to a destination and back to the airport.

a) Calculate the amount in UG Shs for a one way ticket to B if the exchange rate is US $ 1 to UGShs  2500/=

b) A family bought four return tickets for destination A at UG Shs 5,737,000. Determine the exchange rate.

c) A tourist bought a one way ticket to C at a rate of US $1 to Ug Shs 2,400. Another tourist bought a one way ticket to C at a rate of US $1 to UG Shs 2,420, a week later. How much more in Ug Shs did the second tourist pay?

17.The diagram below shows a cuboid KLMNWXYZ in which

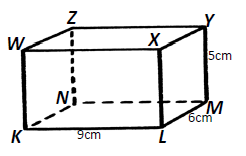
a) Calculate the length

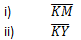
b) Determine the angle between: