SECTION A
1. If 125n = 85ten, find n.
2. In a group of 29 girls, 22 liked Rice (R) and 18 liked Matoke (M). All girls liked at least one of the foods. How many liked both?
3. Solve the inequality: 10 - 3x < 4(x - 1).
4. Without using mathematical tables or a calculator, evaluate:
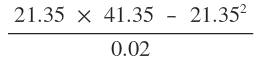
5. Two quantities y and x are related by the equation y = a + bx. When y = 4, x = 2 and when y = 6, x = 4. Find the values of a and b.
6. Given that sin a = 3/5 and a is obtuse, without using mathematical tables or calculator, find the values of cos a and tan a.
7. A shop keeper bought an item at shs5,500 and sold it at 30% more than the buying price. Find the shopkeeper's.
a) Selling price
b) Profit
8. Given the matrix P = 
, find P2.
9. Use tables of logarithms to evaluate:
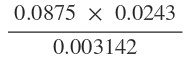
10. Solve the following pairs of simultaneous equations
5x - 9y = 1,
4y - 2 = x.
SECTION B
Answer any five questions from this section, all questions carry equal marks.
11. The following table shows marks obtained by 40 pupils in a mathematics test.
| 11 | 17 | 35 | 34 | 42 | 45 | 28 | 46 |
| 16 | 12 | 14 | 36 | 41 | 31 | 49 | 37 |
| 20 | 33 | 37 | 38 | 18 | 38 | 39 | 27 |
| 26 | 28 | 40 | 33 | 43 | 32 | 29 | 47 |
| 29 | 32 | 41 | 24 | 44 | 35 | 36 | 23 |
a) Draw a frequency distribution table for the marks, starting with a class of 10 - 14.
b) State the:
(i) Class interval,
(ii) Modal class.
c) Calculate the:
(i) Mean mark,
(ii) Median mark.
12. a) (i) Determine the range corresponding to the domain.
(-3, -2, 0, 1, 3, 4) for the mapping x →x2 + 1.
(ii) Represent the mapping in (i) on an arrow diagram.
b) Given the functions h(x) = x + 2, g(x) = x2 and f(x) = -x; find the values of x for which g [h(x)] = f(x).
13. A triangle with vertices A (2, 4), B (6, 4) and C (1, 6), undergoes two successive transformations P1 followed by P2. The transformation P1 is represented by the matrix 
and P2 by the matrix 
a) find the co-ordinates of the vertices of:
(i) Triangle A'B'C' the image of ABC under P1.
(ii) Triangle A"B"C" the image of A'B'C' under P2.
b) Show on the same axes the three triangles ABC, A'B'C' and A"B"C".
c) Use your graph in (b), to describe fully the transformations represented by
(i) P1,
(ii) P2.
14. a) A student had his rectangular photograph of dimensions 30 cm by 20 cm framed with a uniform border. If the area of the border is 216 cm2, how wide is the border?
b) A cone has a radius of 7 cm and a vertical height of 30 cm. find:
(i) Its volume, 
(ii) The volume of another similar bigger cone which has a linear scale factor of 2.
15. a) Find the equation of a line passing through a point (2,0) and perpendicular to the line joining the points (-10,3) and (6, -9)
b) A triangle PQR has vertices with coordinates P(3,-1), Q(7,6) and R(0,2). Find the equation of its line of symmetry.
16. A hawker sells handkerchiefs at shs500 each. He sold 50 handkerchiefs in the first week. In the second week he sold 20% more than in the first week. In the third week he sold 10% more than in the second week. Each week he receives a commission of 8% on the price of the first 20 handkerchiefs sold and 12% for any handkerchiefs sold in excess of 20.
a) Express the number of handkerchief sold in the third week as a percentage of the number sold in the first week.
b) Calculate the commission he received in the third week.
c) If in the fourth week the hawker received a commission of 2,000/= calculate the number of handkerchiefs he sold in that week.
17. In the diagram below, OA = a, OB = b, 
=1:3, 3OF = 2OA and E divides AC in the ratio 3:2.
TRIANGLE
Express the following vectors in terms of a and b.
a) BC.
b) CA.
c) BE.
d) FE.
PAPER 2
SECTION A
1. Express 0.341666... in the form p/q, where q ≠0.
2. Solve for x in 323/5 ÷ x1/2 = 2.
3. Given two points P (4, 5) and Q (-2, 9), find the equation of the line through P and q.
4. Simplify 
. Give your answer in the form 
where a and b are constants.
5. A rectangle 6cm long and 5cm wide is enlarged so that its area becomes 270cm2. Find the linear scale factor of the enlargement.
6. In the figure below, O is the centre of the circle, angle JKQ = 400 and KOQ is a straight line.
CIRCLE
Find the angles marked n and p.
7. Given that a = 
, b = 
and m = a + 2b, find the magnitude of m.
8. If n = x 
, express m in terms of n and x.
9. A function f(x) = 
. Find the values of x for which f(x) = 4.
10. Three girls, Auma, Assimwe and Nakato shared shs10, 500. Nakato got twice as much as Assimwe and Assimwe got twice as much as Auma. Find how much money Assimwe got.
SECTION B
Answer any five questions from this section. All questions carry equal marks.
11. A speed boat sets off from an island M on a bearing of 0800 to an island X at an average speed of 150kmh-1, island X is 450 km from island M. at X it alters its course to a bearing of 2000 and maintains the average speed of 150kmh-1 for 3 hours until it reaches island Y. it then moves to island P is 400 km from island M.
a) Using a scale of 1 cm to represent 50 km, construct a scale drawing to show the route of the speed boat.
b) Use the scale drawing in (a) to find the distance PY.
c) Calculate the
(i) Total time taken for the speed boat to move from M to P.
(ii) Speed boat's average speed for the whole journey.
12. The Venn diagram below shows the members of a district council who sit on three different committees of works (W), production (P) and Finance (F).
VENN DIAGRAM
a) Determine the value of x, y and z.
b) Find the total number of members who
(i) Make up the district council.
(ii) Belong to more than one committee.
c) Given that a member is selected at random from the district council, find the probability that the member belongs to only two committees.
13. a) express 
in the form 
b) A mini bus travels from migyera to Kampala, a distance of 156km, at a certain average speed of Vkm/hr. on the return journey, it increases the average speed by 4 km/hr and takes 15minutes less. Find the average speed V from Migyera to Kampala.
14. The table below shows time (t) in seconds and velocity (V) in m/s of an object.
| t(s) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| V(m/s) | 0.0 | 1.0 | 1.7 | 2.0 | 1.7 | 1.0 | 0.0 |
a) Using a scale of 2cm to represent one second on the horizontal axis and 4cm to represent 0.5 m/s on the vertical axis, plot the values of t and V and join the points with a smooth curve.
b) Use your graph in (a), to find the
(i) Times at which the speed of the object is 0.8 m/s.
(ii) Acceleration of the object when the time is 2 seconds.
c) If the total distance covered by the object was 7.5m, what was its average speed?
15. a) without using mathematical tables or a calculator, find the value of
2 log 10 50 + log 10 80 - log 10 2.
b) (i) find the prime factors of 150.
(ii) Using your result in (i), find log 10150, given that
Log 10 5 = 0.6990, log 10 3 = 0.4771 and log 10 2 = 0.3010.
16. a) solve the following simultaneous equations using the matrix method
5x + 2y = 5,
3x - 0.2y = 10.
b) Given that P= 
, Q= 
and R = 
;
Find:
(i) QR - P,
(ii) The determinant of QR - P.
17. Mr. Oketcho's monthly gross salary is shs900,000 which includes the following allowances:
Shs
Water and electricity 20,000
Relief and insurance 30,000
Housing allowances 50,000
Medical allowance 25,000
Transport allowance 28,000
Marriage allowance 20,000
Family allowance
(for only 4 children):
- From 0 to 9 years 20,000 per child
- Between 9 and 16 years 15,000 per child
- Over 16 years 10,000 per child
Mr. Oketcho has five children; two of whom are aged between 0 and 9 years, one aged 14 years and the other two are over 16 years.
The income tax structure is shown in the table below:
| Taxable income per month in shillings. | Tax rate % |
| 01 - 50,000 50,001 - 110,000 110,001 - 200,000 200,001 - 350,000 350,001 - 600,000 Above 600,000 |
10.0 20.0 24.5 35.0 40.0 49.0 |
a) Calculate Mr. Oketcho's
(i) taxable income
(ii) Income tax
b) Express the income tax as a percentage of his monthly gross salary.