SECTION A
1. Write down the next term of each of the given sequences;
(i) 2, 3, 1, 4, 0, ...........
(ii) 1, 4, 20, 120, .......
2. Without using tables or calculator find the value of
(i) Cos 7800,
(ii) Sin 3900.
3. Without using tables or calculator, simplify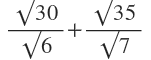 
4. At lunch time a certain hotel received 80 customers. Of these 45 had a posho (P) meal and 50 had Matoke (M).
(i) Represent this information in a Venn diagram
(ii) Find the number of people who had a meal of both P and M.
5. If the point P(2, -1) undergoes a translation represented by the matrix 
find the image of P.
6. Calculate the simple interest on shs96,000 for 10 months at a rate of 81/3% per annum.
7. Use mathematical tables to evaluate (0.48)3/5 correct to 2 decimal places.
8. A stretch of land on a map of scale 1:15,000 has an area of 300 cm2. Determine the actual area of the land in km2.
9. A floor measuring 6m x 4m is to be covered with square tiles measuring 50 cm each. Find the cost of covering the floor. If the price of a dozen of the tiles is shs15,000.
10. Show that the points (3x, -2y), (2x, y) and (0, 7y) lie on a straight line.
SECTION B
Attempt any five questions from this section. All questions carry equal marks.
11. a) Express x2 + x - 12 in the form (x+a)2+ b. hence solve the equation x2 + x - 12 = 0.
b) Given the functions f(x) =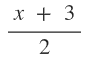 
and g(x) = 
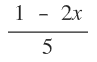. Determine the values of x for which fg(x) =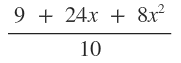 
12. a) use matrix methods to solve the following pair of simultaneous equations:
x + y = 3,
3x - 2y + 1 = 0.
b) A transformation maps (1, 2) onto (-1, 4) and (2, 3) onto (-1, 7).
(i) Find the matrix of this transformation.
(ii) Determine the image of (3, 0) under this transformation.
13. Using a ruler, pencil and pair of compasses only,
(i) Construct a triangle ABC such that 
=8.7 cm, 
= 10.6 cm and angle BAC = 600,
(ii) Inscribe a circle on the triangle ABC,
(iii) Construct a perpendicular from B onto to meet it at point D.
(iv) Measure length 
and the radius of the circle
(v) Measure 
and calculate the area of triangle ABC.
14. The figure below shows a hollow pipe of external diameter 16mm, internal diameter 10 mm and length 50cm.
FIGURE
(i) Calculate the surface area (in cm2) of the pipe correct to decimals places. 
(ii) What would be the surface area of a similar pipe of length 150 cm, external diameter 48 mm and internal diameter 30 mm?
15. The table below shows the marks obtained in a chemistry test by S4 student in a certain school.
| 54 | 49 | 60 | 58 | 54 |
| 60 | 51 | 57 | 56 | 54 |
| 53 | 59 | 56 | 52 | 55 |
| 57 | 62 | 54 | 54 | 56 |
| 48 | 51 | 52 | 55 | 58 |
| 65 | 55 | 54 | 57 | 61 |
a) Using class widths of 3 marks and starting with the 48-50 class, make a frequency distribution table.
b) Use your table to
(i) Draw a histogram
(ii) Determine the median and mean marks.
16. a) Okello bought 3 pens and 2 rulers from a book shop at shs3.150. Mukasa bought 2 pens and 3 rulers from the same bookshop at shs2,850.
(i) Find the cost of each pen and ruler.
(ii) If Mugisha spends shs6,000 to buy n pens and n rulers, find n.
b)a pick up van can be bought by cash at shs8,750,000 or can be bought on hire purchase by paying a 25% deposit of the cash price and 12 monthly installment of shs600,000 per month.
Calculate the:
(i) Cost of the pick up by hire purchase.
(ii) Extra money paid for the pick up by hire purchase than by cash.
17. A transport company has 8 Lorries of 8 tones carrying capacity each, and 5 Lorries of 10 tones capacity each. There are 12 drivers available. The company was contracted to transport 480 tones of cement from the factory to a town on a given day. The 8 tone Lorries can make 6 journeys in a day and the 10 tone Lorries 4 journeys a day. The costs of using an 8 tone lorry and a 10 tone lorry are shs40,000 and shs60,000 respectively.
(i) Write down four inequalities to represent the above information.
(ii) Plot a graph for the inequalities, shading out the unwanted regions.
(iii) From your graph find the numbers of 10 tone and 8 tone Lorries the company used, keeping its costs as minimal as possible.